What is an eigencircle of a 2x2 matrix?
Bottom-up definition of an eigencircle
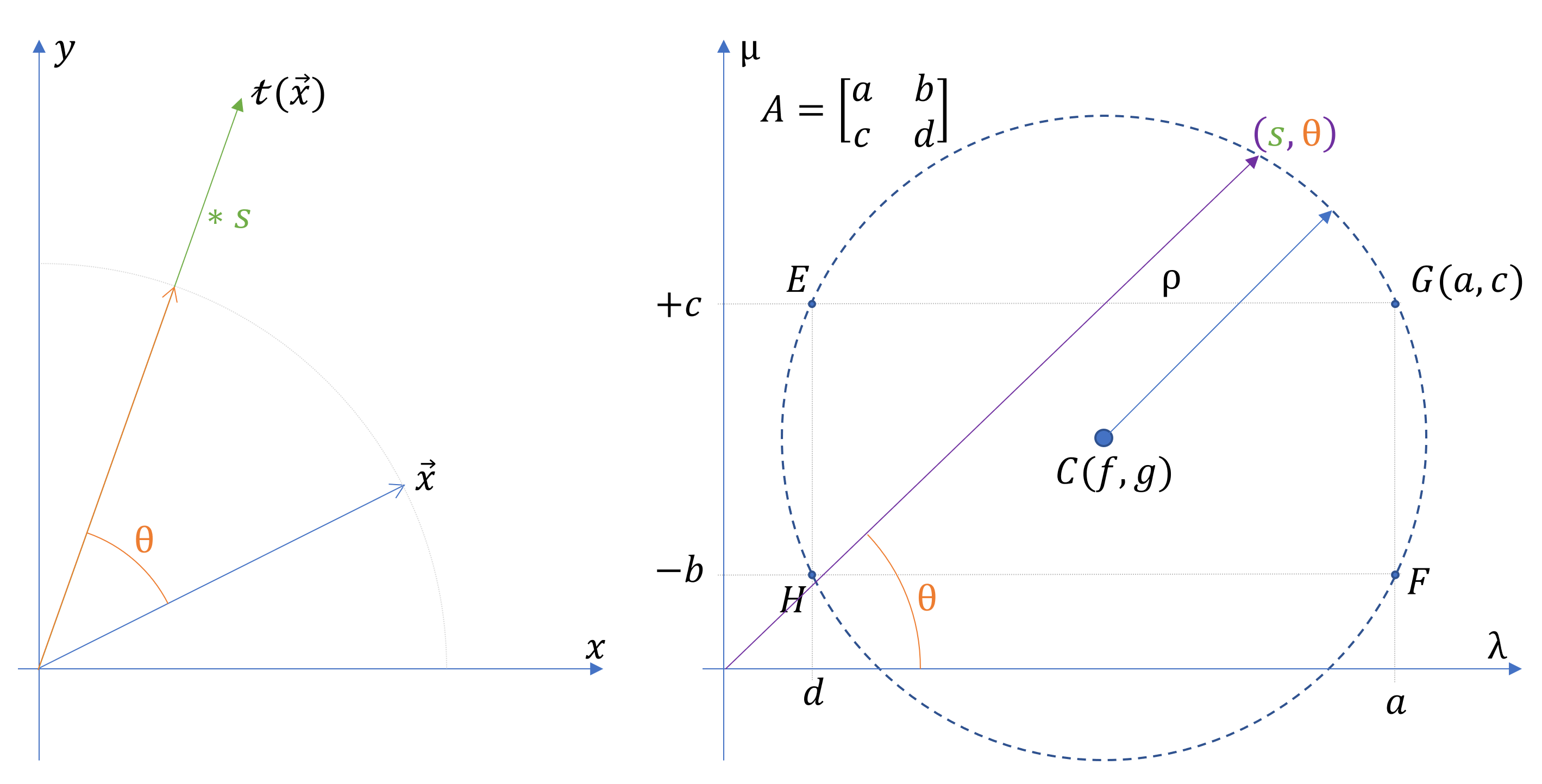
If \(\mathfrak{t}\) is a linear transformation, the relation between a vector \(\vec{x}\) and its image \(\mathfrak{t}\left(\vec{x}\right)\) can be described as
rotating the original vector until it is collinear with \(\mathfrak{t}\left(\vec{x}\right)\) and
scaling until its length is the same as the length of \(\mathfrak{t}\left(\vec{x}\right)\).
For each vector \(\vec{x}\) this effect can be described as a tuple \((s,\theta)\) where s is the scaling and θ the rotation.
The set of all possible couples of rotation and scaling \(\left(s,\theta\right)\ \)is a circle.
This circle is called the eigencircle of the linear transformation \(\mathfrak{t}\).
Top-down definition of an eigencircle
The eigencircle of a linear transformation \(\mathfrak{t}\) is a circle defined by all possible tuples \((s,\theta)\)
where
\(\theta=\angle\left(\vec{x,}\mathfrak{t}\left(\vec{x}\right)\right)\) is the angle between an original vector \(\vec{x}\) and its image \(\mathfrak{t}\left(\vec{x}\right)\ \)and
\(s=\frac{\|\mathfrak{t}(\vec{x})\|}{\|\vec{x}\|}\) is the scaling \(s\) from the original length \(\|\vec{x}\|\) to the final length \(\|\mathfrak{t}(\vec{x})\|\).
Formal denotation of an eigencircle
\({EC(\mathfrak{t})}_{polar}=\left\{\left(\ s_{\vec{x}},\theta_{\vec{x}}\right)\ |\ \exists\vec{x}=\left[\begin{matrix}x\\y\\\end{matrix}\right]\ and\ \mathfrak{t}\left(\vec{x}\right)=\left[\begin{matrix}s_{\vec{x}}&0\\0&s_{\vec{x}}\\\end{matrix}\right]\left[\begin{matrix}\cos{\theta_{\vec{x}}}&-\sin{\theta_{\vec{x}}}\\+\sin{\theta_{\vec{x}}}&\cos{\theta_{\vec{x}}}\\\end{matrix}\right]\left[\begin{matrix}x\\y\\\end{matrix}\right]=A\left[\begin{matrix}x\\y\\\end{matrix}\right]\right\}\)
\({EC(\mathfrak{t})}_{polar}=\left\{\left(s_{\vec{x}},\theta_{\vec{x}}\right) |\ \exists \vec{x}\ such\ that\ s_{\vec{x}}=\frac{\|\mathfrak{t}(\vec{x})\|}{\|\vec{x}\|} \ and\ \theta_{\vec{x}}=\angle(\vec{x},\mathfrak{t}(\vec{x}))\right\}\)
\({EC(\mathfrak{t})}_{cart}=\left\{\left(\lambda,\mu\right)\ |\ \exists\vec{x}=\left[\begin{matrix}x\\y\\\end{matrix}\right]and\ \mathfrak{t}\left(\vec{x}\right)=\left[\begin{matrix}\lambda&-\mu\\+\mu&\lambda\\\end{matrix}\right]\left[\begin{matrix}x\\y\\\end{matrix}\right]=\left[\begin{matrix}s_{\vec{x}}&0\\0&s_{\vec{x}}\\\end{matrix}\right]\left[\begin{matrix}\cos{\theta_{\vec{x}}}&-\sin{\theta_{\vec{x}}}\\+\sin{\theta_{\vec{x}}}&\cos{\theta_{\vec{x}}}\\\end{matrix}\right]\left[\begin{matrix}x\\y\\\end{matrix}\right]\right\}\)
Can I find the eigenvalues and eigenvectors of a matrix in a geometric way?
Using the concept of an eigencircle the eigenvalues and eigenvectors of a 2x2-matrix can be derived.
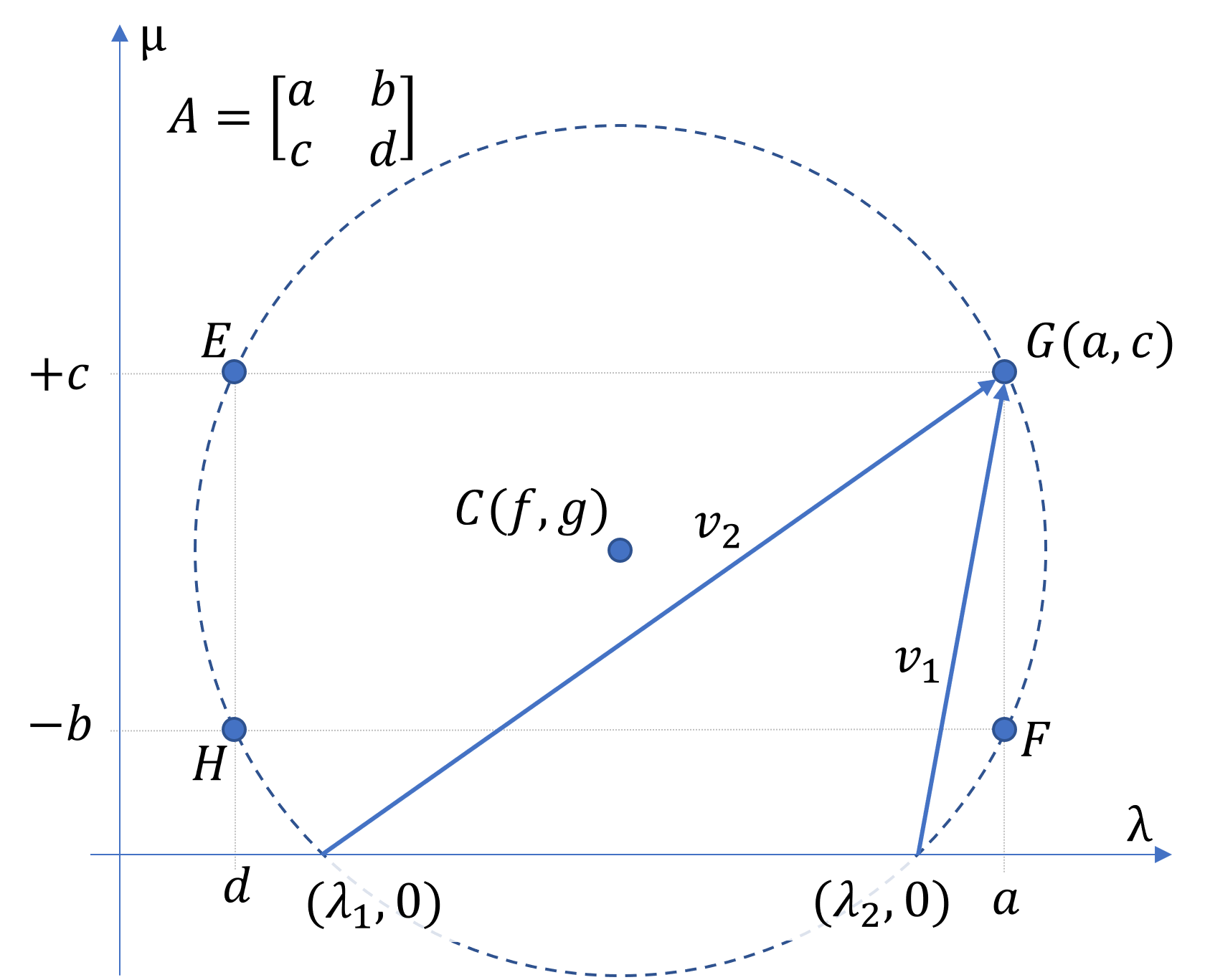
If the eigencircle of a matrix is constructed using the steps below, the eigenvectors and eigenvalues can be read from the geometric construction.
Construct the circle with center \(C(f,g)\) and radius \(\rho\).
|
\(f=\frac{\left(a+d\right)}{2}\) |
||
|
\(g=\frac{\left(c-b\right)}{2}=-\frac{\left(b-c\right)}{2}\) (The value of g is the negation of the formula in the articles) |
||
|
\(\rho^2=\left(\frac{a-d}{2}\right)^2+\left(\frac{b+c}{2}\right)^2\) |
|
Eigencircle of A: \(\left(\lambda-f\right)^2+\left(\mu-g\right)^2-\rho^2=0\) |
Who defined the concept 'eigencircle'?
The concept eigencircle is described in two articles by EngleField and Farr.
Englefield, M. J., & Farr, G. E. (2006). Eigencircles of 2 x 2 Matrices. Mathematics Magazine Vol. 79 Oct.,2006, 281-289.
Englefield, M. J., & Farr, G. E. (2010). Eigencircles and associated surfaces. The Mathematical Gazette Vol.94 No. 531 (November 2010), 438-449.

